데이터 파일 구성
① train.csv : 서울시 마포구의 날짜별, 시간별 기상상황과 따릉이 대여 수 (기간: 2017년 4월, 5월)
② test.csv : count 외에는 train 데이터와 동일
③ submission.csv : submission 파일의 예시
날씨로 한 시간 후의 자전거 대여 수 예측하기
- 고유id
- 시간
- 기온
- 비가오지 않았으면0,비가오면1
- 풍속평균
- 습도
- 시정(視程), 시계(視界)(특정 기상 상태에 따른 가시성을 의미)
- 오존
- 미세먼지(머리카락 굵기의 1/5에서 1/7 크기의 미세먼지)
- 미세먼지(머리카락 굵기의 1/20에서 1/30 크기의 미세먼지)
- 시간에 따른 따릉이 대여 수
import pandas as pd
import numpy as np
#데이터 불러오기
train=pd.read_csv('train.csv')
test=pd.read_csv('test.csv')
submission=pd.read_csv('submission.csv')
train.head()
test.head()
submission.head()
print(train.shape,test.shape,submission.shape)
#결측값 확인
train.info()
test.info()
#컬럼별 기술 통계량 구해보기
train.describe()
test.describe()- shape 결과
train (1459, 11) test (715, 10) submission (715, 2)
- info() 결과

각 컬럼에 빈값이 있는지 확인한다.
temoerature,precipitation 등 각 칼럼에 null 인 값이 몇개씩 있다.
- describe() 결과

각 컬럼에 따른 null이 아닌값 수, 평균값, 표준편차, 최대 최소, 사분위수가 표시된다.
이상치가 있는지 확인한다.
이상치
max>Q3+IQR*1.5 | min<Q1-IQR*1.5 (IQR=Q3-Q1)
이 데이터에서는 딱히 없는것 같다.
count by hours 그래프 확인
import matplotlib.pyplot as plt
plt.plot(train.groupby('hour').mean()['count'],'go-')
plt.grid()
plt.title('count by hours',fontsize=15)
plt.xlabel('hour',fontsize=10)
plt.ylabel('count',fontsize=10)
plt.axvline(8,color='r')
plt.axvline(18,color='r')
plt.text(8,120,'go work',fontsize=10)
plt.text(18,120,'leave work',fontsize=10)
plt.savefig('count_by_hours.png')
출퇴근시간에 사용자가 많음을 알 수 있다.
이런식으로 그래프로 상관관계를 확인하는 방법은 한계가 있다. 그래프에서 보고 우리가 예측한것과 달리 결과값과 상관이 없는 계수가 있을 수 있기 때문이다. 이러한 계수는 모델에 악영향을 줄 수 있기 때문에 보다 계수선택을 잘 하기 위해 각 계수들의 상관계수를 알아보자
상관계수
두 개의 변수가 같이 일어나는 강도를 나타내는 수치
-1에서 1사이 값이며 보통 0.4 이상일 경우 두 개의 변수간에 상관성이 있다고 한다.
상관관계가 있다고 해서 인과관계가 있지는 않다.
모델을 생성하는데 있어 좋은 변수들을 골라내기 위해 가장 간단한 방법이 상관계수가 높은변수들을 골라서 모델을 생성하는것이다.
#다음 코드로 간단히 확인할 수 있다.
train.corr()
import seaborn as sns
plt.figure(figsize=(10,10)) # 크기 설정
sns.heatmap(train.corr(),annot=True) # annot: 숫자 표시
데이터 전처리
사용할 변수
- hour
- hour_bef_temperature
- hour_bef_windspeed
#결측치 확인
train.isna().sum()#컬럼별 null 값의 수
train[train['hour_bef_temperature'].isna()]#온도가 null인 행 출력
#시간에 따른 온도 그래프에 전체 시간에서의 온도평균 그래프를 겹쳐서 확인한다.
train.groupby('hour').mean()['hour_bef_temperature'].plot()
plt.axhline(train.groupby('hour').mean()['hour_bef_temperature'].mean())
#시간에 따른 온도 평균값
train.groupby('hour').mean()['hour_bef_temperature']
#null값을 채운다. fillna 함수 사용. inplace옵션을 True로 해준다.
train['hour_bef_temperature'].fillna({934:14.788136,1035:20.926667},inplace=True)
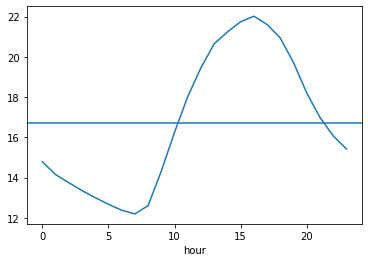
같은 방법으로 풍속과 test 에서의 온도 풍속의 null 값도 채워준다.
모델링
X를 입력 받아 Y를 산출
#모델에서 사용할 계수와 결과 컬럼만 뽑아서 저장해 놓는다.
features=['hour','hour_bef_temperature','hour_bef_windspeed']
X_train=train[features]
Y_train=train['count']
X_test=test[features]
#랜덤포레스트 방법을 사용해본다.
from sklearn.ensemble import RandomForestRegressor
#랜덤포레스트에서 하이퍼 파라미터를 조정한 3개의 모델을 생성한다.
model_100=RandomForestRegressor(n_estimators=100,random_state=0)
model_100_5=RandomForestRegressor(n_estimators=100,max_depth=5,random_state=0)
model_200=RandomForestRegressor(n_estimators=100,random_state=0)
#모델에 train 의 x,y를 넣어 학습한다.
model_100.fit(X_train,Y_train)
model_100_5.fit(X_train,Y_train)
model_200.fit(X_train,Y_train)
#학습한 모델에 test x를 넣어 결과를 뽑는다.
ypred1=model_100.predict(X_test)
ypred2=model_100_5.predict(X_test)
ypred3=model_200.predict(X_test)
#결과값을 csv 파일로 저장한다.
submission['count']=ypred1
submission.to_csv('model100.csv',index=False)
submission['count']=ypred2
submission.to_csv('model100_5.csv',index=False)
submission['count']=ypred2
submission.to_csv('model200.csv',index=False)
# 제출결과 점수는 RMSE 라는 오차로서 작을수록 좋다.jupyter notebook에서 함수 설명은 shift+tap을 눌러 확인할 수 있다.
랜덤포레스트
분류, 회귀 분석 등에 사용되는 앙상블 학습 방법의 일종으로, 훈련 과정에서 구성한 다수의 결정 트리로부터 부류(분류) 또는 평균 예측치(회귀 분석)를 출력함으로써 동작한다.
하이퍼 파라미터
모델링할 때 사용자가 직접 세팅해주는 값
하이퍼 파라미터를 잘 사용하기 위해 모델에 대한 이해가 필요하다. 데이터 전처리와 선택한 계수,그리고 이 값들이 모델의 성능을 좌우한다.
평균 제곱근 편차(Root Mean Square Deviation; RMSD) 또는 평균 제곱근 오차(Root Mean Square Error; RMSE)
추정 값 또는 모델이 예측한 값과 실제 환경에서 관찰되는 값의 차이를 다룰 때 흔히 사용하는 측도이다.
잔차의 제곱의 평균의 제곱근이다.....

단순히 따라 친다고 해서 늘 것 같진않다.
대략적으로 해야되는 것을 정리하자면...
1. 데이터의 상태 확인
2. 데이터에 대한 이해 목표값과 각 칼럼의 의미 및 형태 등등...
3. 목표값과 각 칼럼의 상관관계 파악을 통해서 모델에 사용할 계수 선정
4. 예측을 위한 모델 선정
5. 모델에 대한 이해 및 하이퍼 파라미터 설정
6. 모델의 예측 결과 확인 및 위 과정 반복을 통해 보다 나은 모델 탐색
댓글